3D.Compute.Generate.Torus

This node generates a torus with a fixed outer radius of 1.0. The tube radius slot allows selecting the inner radius in percentage of the outer radius.

torus_20_50.png

The image above shows two tori with tube radius 20% (left) and tube radius 50% (right).

3D.Compute.Generate.TorusKnot

This node generates a torus knot. The knot is constructed from a 3D curve that twines around an imagined torus. The imagined torus has a fixed outer radius of 1.0 and its inner radius can be selected via the torus radius slot in percentage of the outer radius. The twinded 3D curve is thickened in order to form a tube. The radius of the tube's cross sections can be selected with the tube radius slot in percentage of the outer radius.

How often the 3D curve twines around the imagined torus is controlled by two integers values p and q. The parameter p can be selected with the winding up/down slot and q with the winding around slot. Some (p-q)-torus knots have special names, e.g. a (2,3)-torus knot is called trefoil knot and a (2,5)-torus knot is called cinquefoil knot.


(1,0)-torus knot
(1,5)-torus knot
(1,7)-torus knot
(1,9)-torus knot
(1,11)-torus knot

(2,3)-torus knot
(2,5)-torus knot
(2,7)-torus knot
(2,9)-torus knot
(2,11)-torus knot

(3,4)-torus knot
(3,5)-torus knot
(3,7)-torus knot
(3,8)-torus knot
(3,11)-torus knot

What follows below is some math that I wrote down while implementing these nodes:

Torus

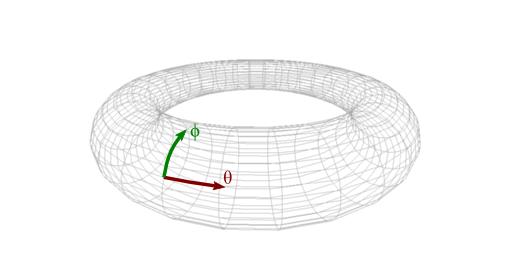
A torus can be constructed from a 2D parameterization in $\theta$ and $\phi$, both in range $[0, 2\pi]$. The variable $\theta$ follows the outer circle, and $\phi$ the inner (cross-section) circles as shown in the image below.

torus_theta_phi

With this parameterization the 3D vertices of a torus are computed by:

$\mathbf{x}(\theta, \phi) = \begin{pmatrix}(1.0 + r \cos(\phi)) \cos(\theta)\\ (1.0 + r \cos(\phi)) \sin(\theta)\\ r \sin(\phi)\\ \end{pmatrix}$,
where $r$ is the radius of the cross-section circles.
In order to compute the 3D surface normals, the tangent directions in $\theta$ and $\phi$ are needed. These are given by the partial derivatives:
$\mathbf{t}_{\theta}(\theta, \phi) = \frac{\partial \mathbf{x}(\theta, \phi)}{\partial \theta} = (1.0 + r \cos(\phi)) \begin{pmatrix} -\sin(\theta)\\ \cos(\theta)\\ 0.0\\ \end{pmatrix}$
$\mathbf{t}_{\phi}(\theta, \phi) = \frac{\partial \mathbf{x}(\theta, \phi)}{\partial \phi} = r \begin{pmatrix} -\sin(\phi) \cos(\theta)\\ -\sin(\phi) \sin(\theta)\\ \cos(\phi)\\ \end{pmatrix}$
The cross product of both tangent directions gives the surface normal
$\mathbf{n}(\theta, \phi) = \mathbf{t}_{\theta} \times \mathbf{t}_{\phi} = \begin{pmatrix} -\sin(\theta)\\ \cos(\theta)\\ 0.0\\ \end{pmatrix}\times \begin{pmatrix} -\sin(\phi) \cos(\theta)\\ -\sin(\phi) \sin(\theta)\\ \cos(\phi)\\ \end{pmatrix} = \begin{pmatrix} \cos(\theta) \cos(\phi)\\ \sin(\theta) \cos(\phi)\\ \sin(\phi) \end{pmatrix} $
because $\sin^2(\theta) + cos^2(\theta) = 1$. The length of this normal is always 1.0.

Torus Knot

The curve of a (p-q)-torus knot is computed from the knot equation above by parameterizing the curve with a single parameter $t$ in the range $[0, 2\pi]$:
$\mathbf{x}(p\,t, q\,t) = \begin{pmatrix}(1.0 + r \cos(q\,t) \cos(p\, t)\\ (1.0 + r \cos(q\,t)) \sin(p \,t)\\ r \sin(q\,t)\\ \end{pmatrix}$
To generate cross-sections perpendicular to the knot curve, we need normal, tangent, and binormal vectors to span a local coordinate system. As the curve twines around the torus that is used for its construction and lies exactly on its surface, we can reuse the formula for the torus normal from above:
$\mathbf{n}'(t) = \mathbf{n}(p\,t, q\,t) = \begin{pmatrix} \cos(p\,t) \cos(q\,t)\\ \sin(p\,t) \cos(q\,t)\\ \sin(q\,t) \end{pmatrix} $
The chain rule for partial derivatives is helpful to compute a tangent direction for $t$:
$\mathbf{t}_{t}(t) = \frac{\partial \mathbf{x}(p\,t, q\,t)}{\partial t} = p \, \mathbf{t}_{\theta}(p\,t, q\,t) + q \, \mathbf{t}_{\phi}(p\,t, q\,t)$
Let $\mathbf{t}_{t}'(t)$ be the normalized tangent vector $\mathbf{t}_{t}(t)$, the binormal is given by:
$\mathbf{b}'(t) = \mathbf{t}_{t}'(t) \times \mathbf{n}'(t)$
Using the local coordinate system, we can generate circles with radius $c$ as cross sections in the plane spanned by $\mathbf{n}'(t)$ and $\mathbf{b}'(t)$. To this end, we introduce a new parameter $s$ in range $[0, 2\pi]$ for the parameterization of the circles. Then the 3D vertices of the (p-q)-torus knot are given by
$\mathbf{x}_{\tiny\mbox{knot}}(s, t) = \mathbf{x}(p\,t, q\,t) + c \, \cos(s) \, \mathbf{n}'(t) + c \, \sin(s) \, \mathbf{b}'(t)$
and its 3D surface normals by
$\mathbf{n}_{\tiny\mbox{knot}}(s, t) = \cos(s) \, \mathbf{n}'(t) + \sin(s) \, \mathbf{b}'(t).$